Journal Menu
Volume 8, Issue 1 (2017), Pages [1] - [79]
SEMILOCALITY AND DENSITY OF MULTI-ANISOTROPIC OBOLEV SPACES
[1] O. V. Besov, On the density of the compactly supported functions in a weighted Sobolev space, Proc. Steklov Inst. Math. 161 (1984), 33-52 (in Russian).
[2] O. V. Besov, V. P. Il’in and S. M. Nikolskii, Integral Representations of Functions and Embedding Theorems, John Wiley and Sons, New York, Vol. 1, 1978; Vol. 2 1979.
[3] V. I. Burenkov, On density of infinite differentiable functions in the Sobolev spaces for arbitrary open sets, Proc. Steklov Inst. Math. 131 (1974), 39-50 (in Russian).
[4] V. I. Burenkov, Sobolev Spaces in Domains, B. G. Teubner, Stuttgart-Leippzig, 1998.
[5] Daniela Calvo, Multi-anisotropic Gevrey Classes and Cauchy Problem, Ph. D. Thesis in Mathematics, Universita degli Studi di Pisa, 2004.
[6] A. Carlson and V. Maz’ya, On approximation in weighted Sobolev spaces and self-adjointness, Math. Scand. 74 (1994), 111-124.
[7] A. Corli, Un teorema di representazione per certe classi generalizzate di Gevrey, Boll. Un. Mat. It., Serie 6, 4 C (1) (1985), 245-257.
[8] H. G. Ghazaryan and V. N. Margaryan, On infinite differentiability of solutions of nonhomogenous almost hypoelliptic equations, Eurasian Math. Journal 1(1) (2010), 54-72.
[9] S. G. Gindikin and L. R. Volevich, The Method of Newton’s Polihedron in the Theory of PDE, Mathematics and its Applications, Soviet Series, Kluwer Academic Publishers, 1992.
[10] L.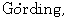 
Linear hyperbolic partial differential equations with constant coefficients, Acta Math. 85 (1951), 1-62.
Linear hyperbolic partial differential equations with constant coefficients, Acta Math. 85 (1951), 1-62.[11] L. Hörmander, The Analysis of Linear Partial Differential Operators, Vol. 1; Vol. 2, Springer-Verlag, 1983.
[12] V. P. Il’in, On inequalities between the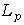 
-norms of partial derivatives of functions in many variables, Proc. Steklov Inst. Math. 96 (1968), 205-242 (in Russian).
-norms of partial derivatives of functions in many variables, Proc. Steklov Inst. Math. 96 (1968), 205-242 (in Russian).[13] G. G. Kazaryan, On almost hypoelliptic polynomials, Doklady Ross. Acad. Nauk Matematika 398(6) (2004), 701-703 (in Russian).
[14] A. G. Khovanskii, Newton polyhedra (algebra and geometry), Amer. Math. Soc. Transl. (2) 153 (1992), 1-15.
[15] A. Kufner, Weighted Sobolev Spaces, John Willey and Sons, New York, 1985.
[16] E. Larson, Generalized hyperbolicity, Ark. Mat. 7 (1967), 11-32.
[17] V. P. Mikhailov, The behavior at infinity of a class of polynomials, Proc. Steklov Inst. Math. 91 (1967), 65-86 (in Russian).
[18] M. Miyake and Y. Hashimoto, Newton polygons and Gevrey indices for linear partial differential equations, Nagoya Math. Journal 128 (1992), 15-47.
[19] S. M. Nikolskii, Proof of uniquness of the classical solution of first boundary value problem, Izv. AN SSSR, Mat. 27 (1963), 1113-1134 (in Russian).
[20] D. H. Phong and E. M. Stein, The Newton polyhedron and oscillatory integral operators, Acta Math. 179 (1997), 105-152.
[21] L. Rodino, Linear Partial Differential Operators in Gevrey Spaces, Word Scientific, Singapore, 1993.
[22] H. Tribel, Interpolation Theory, Function Spaces, Differential Operators, Veb Deutshcer Verlag der Wissenschaften, Berlin, 1978.
[23] H. Yamazawa, Newton polyhedrons and a formal Gevrey spaces, Funcialaj Ekvacioj 41 (1998), 334-345.